חלוקת ריבוע לריבועים קטנים - למורה
משימה
- האם ניתן לחתוך ריבוע ל-4 ריבועים קטנים?
- האם ניתן לחתוך ריבוע ל-9 ריבועים קטנים?
- האם ניתן לחתוך ריבוע ל-34 ריבועים קטנים?
מדרגה
- הציעו דרכים לחלוקה של ריבוע ל- 7 ריבועים קטנים? ל- 10 ריבועים קטנים?
- הציגו את החלוקות בעזרת סרטוט.
- כמה ריבועים נוספו בכל חלוקה?
- האם ניתן להמשיך בחלוקות הנ״ל?
- הציעו הכללה למספרי הריבועים שהתקבלו.
הנחיות למורה
כיתה מומלצת
- כיתה ז', שליש ראשון.
סוג המשימה
- בעיית חקר.
- ריבוי דרכי פתרון.
הידע הדרוש
- הגדרה ותכונות של ריבוע.
- חשבון של חזקות ברמה בסיסית.
מה נלמד
- חוקיות.
- הכללה של תופעות מספריות.
הדגשים ומטרות
- ההשפעה של כל חלוקה או מחיקה על מספר הריבועים.
- התאמת ביטויים אלגבריים לחלוקות מוצעות.
- חלוקות שונות מתאימות לביטויים זהים.
- חלוקה אחת מתאימה לביטויים שונים.
מערך דידקטי מומלץ
- הצגת המשימה לתלמידים ואופן העבודה.
- עבודה של התלמידים בקבוצות על סעיפים א׳ וב׳.
- דיון כיתתי: חשוב להציג גם את התרשים שמוביל לפתרון.
- עבודה בקבוצות על סעיף ג׳.
- דיון כיתתי מסכם בו יעלו התלמידים את הצעותיהם.
- הצעה להרחבה של האפשרויות– מחיקה של חלוקות.
הצעות לפתרונות:
הערה מקדימה: התלמידים שמשתתפים בפעילות לא בהכרח מכירים את מושג המשתנה.
לכן כדאי להסביר להם את הפתרון באופן מילולי וללא שימוש במשתנה \(n\).
יוצאים מריבוע אחד.
את הריבוע הזה ניתן לחלק ל- 4 ריבועים באופן הבא:
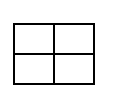
כל אחד מהריבועים הקטנים ניתן לחלוקה לארבעה ריבועים באופן הבא:
כך נוספים 3 ריבועים חדשים בכל חלוקה:
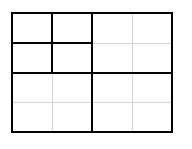
מתקבלים 7 ריבועים

מתקבלים 10 ריבועים.
אם נמשיך בחלוקות הללו נקבל את מספרי הריבועים הבאים:
\(1, \space4,\space7,\space10,\space13,\space16,\space19,\space22,\space25,………\)
מספר הריבועים שכל חלוקה יוצרת מהווים סדרה חשבונית עם איבר כללי \(3n-2\).
באופן דומה ניתן
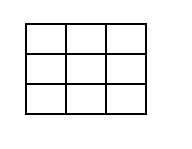
כל אחד מהריבועים הקטנים, שוב ניתן לחלוקה לארבעה ריבועים, באופן הבא:
כך נוספים 3 ריבועים חדשים בכל חלוקה:
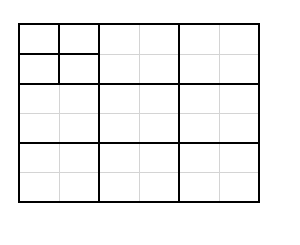
מתקבלים 12 ריבועים
מתקבלים 15 ריבועים
אם נמשיך בחלוקות הללו נקבל את מספרי הריבועים הבאים:
\(9,\space12,\space15,……\)
מספר הריבועים שכל חלוקה יוצרת (חוץ מהריבוע ה- 1) מהווים סדרה חשבונית עם איבר כללי \(3n\), כאשר \((n≥3)\).
שוב יוצאים מריבוע שמחולק ל- 9 ריבועים קטנים.
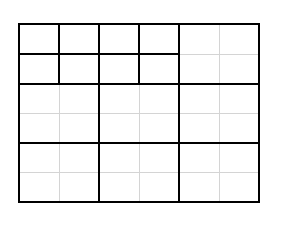
נמחק חלוקה אחת (2×2) מריבוע שמורכב מ- 9 ריבועים קטנים (בדומה לחלוקה שעשינו קודם)
מתקבלים 6 ריבועים
ואם נשלב את שני המהלכים האחרונים שמתייחסים לריבוע המחולק ל- 9 ריבועים קטנים, מתקבלים המספרים:
\(6,\space9,\space12,\space15,\space18,……..\)
כלומר האיבר הכללי נשמר והוא \(3n\), כאשר \((n≥2)\).
נצא שוב מריבוע אחד. הפעם נחלק אותו ל- 16 ריבועים קטנים.
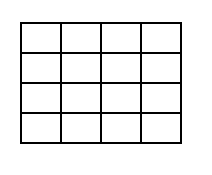
כל אחד מהריבועים הקטנים שוב ניתן לחלוקה לארבעה ריבועים באופן הבא:
כך נוספים 3 ריבועים חדשים בכל חלוקה:

מתקבלים 19 ריבועים
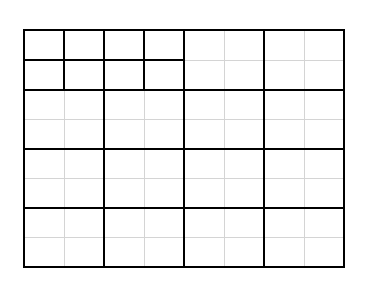
מתקבלים 22 ריבועים
אם נמשיך בחלוקות הללו נקבל את מספרי הריבועים הבאים:
\(16,\space19,\space22,…….\)
חלוקות למספרי הריבועים הללו התקבלו כבר קודם.
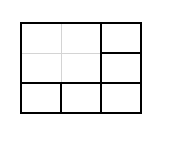
אבל, אם נמחק את החלוקה של 3×3 באופן הבא:

מתקבלים 8 ריבועים
ונמשיך בחלוקות של הריבועים הקטנים:

מתקבלים 11 ריבועים
אם נמשיך נקבל את החלוקות הבאות:
\(8,\space11,\space14,\space17,\space20,\space23,\space26,\space29,\space32,\space35,………\)
מספר הריבועים שכל חלוקה יוצרת (חוץ מהריבוע ה- 1) מהווים סדרה חשבונית עם איבר כללי \(3n+2\), כאשר \((n≥2)\).
לסיכום: בעזרת שילוב של חלוקות ומחיקות מתקבלים כל המספרים הבאים:
\(4,\space6,\space7,\space8,\space9,\space10,\space11,\space12,\space13,\space14,\space15,\space16,…..\)
לא ניתן להגיע למספרים: \(2,\space 3,\space 5\).
אז איך מתקבלים 34 ריבועים?
אם יוצאים מריבוע שחולק ל- 4 ריבועים קטנים – האיבר הכללי שהתקבל הוא:
\(3n-2\), והצבה של 12 תביא אותנו ל- 34.
לאור זאת,
האם ניתן לחלק ריבוע ל- 200 ריבועים קטנים?
הציעו דרכים לחלוקה.
(שאלה זו או דומה לה ניתנת להצגה גם לתלמידים, על פי שיקול הדעת של המורה).


















