أنواع المثلثات أ - درجة
درجة
للبندين 2 و 3
- جدوا في الرسم قطع متساوية بالطول.
- جدوا في الرسم زوايا متساوية.
مهمة
معطى أنّ المثلث ABC هو مثلث متساوي الاضلاع. مدّوا أضلاع المثلث بحيث أن: CF = BE = AG. وصلوا النقاط F ,E و G. النقاط ,P N و M هي نقاط التقاطع بين أضلاع المثلث GFE, وبين القطع FB, AE و GC. (انظروا الرسم بالتطبيق المرفق).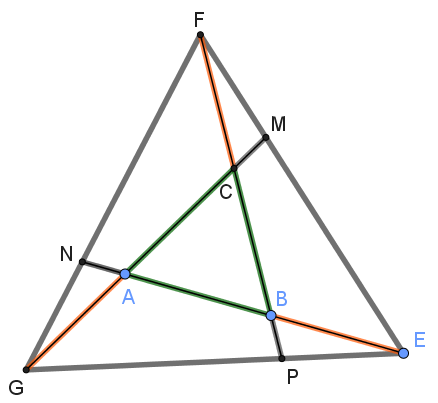
- جدوا عدد المثلثات التي في الرسم المُرفق.
- صنّفوا المثلثات التي في الرسم بطرق مختلفة.
- على أي قيم يمكن أن تحصل الزاوية EFP؟ فسروا إجابتكم.
مثلث
- يمكن إزاحة النقاط باللون الأزرق: A , B, E وتغيير قياسات المثلث بالملائمة.
- يمكن عرض الزاوية EFP.
- لقياس زاوية في المثلث، اضغطوا في مسطرة الأدوات أعلاه على رمز الزاوية
وأشيروا بواسطة الفأر 3 نقاط باتجاه عقارب الساعة.
يتم عندها عرض مقدار الزاوية التي أشرتم الى رأسها. - لقياس طول قطعة ، اضغطوا في مسطرة الأدوات على الرمز لقياس طول قطعة
وأشيروا بواسطة الفأر على النقطتين اللتين هما طرفي القطعة التي تريدون قياس طولها.
يتم عندا عرض طول القطعة التي أشرتم اليها.
جدول التصنيف
- اكتبوا اسم التصنيف في الخانة الملائمة في رأس العمود.
- يمكنكم الاستعانة بالرمز”ABC” الموجود في مسطرة الأدوات أعلاه واكتب اسم المثلث (مثال ABC). بعد ذلك، يمكنكم جرّ هذا اسم المثلث الى العمود الملائم في الجدول.