שלוש נקודות - חלק ג - למורה
משימה
נתונות שלוש נקודות: \(A(5,0)\space\space,\space\space B(0,0)\space\space,\space\space C(6,4.5)\)
- מצאו את שטח משולש ABC.
- מצאו את אורך הגובה לצלע BC.
- נתונה נקודה \(G(-1,3)\). נקודה זו מקיימת: \(S_{\triangle{CBG}}=S_{\triangle{CBA}}\).
האם ישנה נקודה נוספת F המקיימת \(S_{\triangle{CBF}}=S_{\triangle{CBA}}\)?
אם לא – נמקו תשובתכם, ואם כן – מצאו שיעורי נקודה/ נקודות נוספות ונמקו תשובתכם.
מדרגות
- סעיף ב:
תוכלו לחשב את אורכה של צלע BC בעזרת משפט פיתגורס. - סעיף ג:
ניתן להיעזר ביישומון המצורף.
- סמנו את שיעורי הנקודה F: השלימו את שיעור x ואת שיעור y. לחצו Enter.
- כשהנקודה F מופיעה במערכת הצירים, ניתן לגרור אותה ולשנות את שיעוריה. שטח המשולש BCF מתעדכן בהתאם.
- סמנו את שיעורי הנקודה F: השלימו את שיעור x ואת שיעור y. לחצו Enter.
- כשהנקודה F מופיעה במערכת הצירים, ניתן לגרור אותה ולשנות את שיעוריה. שטח המשולש BCF מתעדכן בהתאם.
הנחיות למורה
כיתה מומלצת
סוג המשימה
- ריבוי תשובות.
- משימה המקשרת בין גאומטריה לאלגברה.
הידע הדרוש
- סימון נקודות במערכת צירים.
- חישוב גובה ושטח של משולש.
- חישוב אורכי קטעים במערכת צירים המקבילים לצירים.
- משפט פיתגורס.
- מציאת שיפוע של ישר.
- מציאת ביטוים לפונקציות קוויות מקבילות על פי שיפוע ונקודה.
- מרחק בין קווים מקבילים.
מה נלמד
- מה מאפיין משולשים בעלי צלע משותפת ושטח שווה.
הדגשים ומטרות
- התמודדות עם שאלות בעלות תשובות רבות וניתוחן, כשמתחילים עם מקרה פרטי ועוברים להכללה.
דירוג אתגר מתמטי
- הפניה לאפשרות להיעזר ביישומונים.
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות).
- דיונים כיתתיים:
- התלמידים יציגו את תשובותיהם ואת הדרכים השונות לפתרון לסעיף א'.
- תלמידים מציגים את תשובותיהם לסעיף ב'.
- דיון בסעיף ג' והגעה להכללה.
הצעות לפתרונות:
סעיף א'
שטח המשולש הוא 11.25 יחידות שטח.
סעיף ב'
מציאת BC על פי משפט פיתגורס: \(\sqrt{6^2+4.5^2}=7.5\)
לכן הגובה לצלע BC שווה ל: \(\large\frac{2\cdot 11.25}{7.5}\normalsize=3\).
סעיף ג'
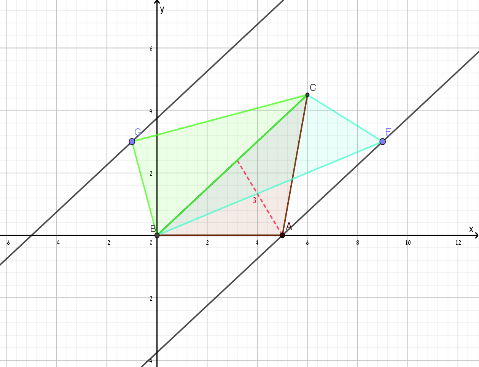
על סמך המשימות שלוש נקודות חלק א' וחלק ב' נצפה שתלמידים יבינו כי קיימות נקודות נוספות והן נמצאות על שני ישרים המקבילים לישר BC ובמרחק 3 יחידות ממנו.
נמצא את משוואת הישר העובר בנקודה G ומקביל לישר העובר בנקודות B ו- C:
לשם כך נחשב את שיפועו של BC: \(\large\frac{4.5}{6}\normalsize=0.75\)
ועל פי הנקודה הנתונה G משוואת הישר היא:
\(y=0.75x+3.75\),
ואז נקודה נוספת לדוגמא על ישר זה היא \((1,4.5)\).
ישר נוסף עובר דרך הקודקוד \((5,0)\) ולכן משוואת הישר השני: \(y=0.75x-3.75\)
ואז נקודה נוספת לדוגמא על ישר זה היא \((9,3)\).