שלוש נקודות - חלק ד - למורה

הנחיות למורה – עברית

משימה לתלמיד – עברית

משימה לתלמיד – بالعربية

מבנה המשימה

محتوى المهمة

משימה

נתונות שלוש נקודות: \(A(3,2)\space\space,\space\space B(3,-4)\space\space,\space\space C(7,1)\)

  1. מצאו את שטח משולש ABC.
  2. מצאו שלוש נקודות היוצרות משולש ששטחו שווה לחצי משטח המשולש ABC, כך ששתיים מהנקודות נמצאות על הישר AB.
  3. האם התשובה לסעיף ב' היא תשובה יחידה?
    אם כן, נמקו תשובתכם,
    אם לא, תארו דרכים שונות למציאת שלוש נקודות על פי התנאים המפורטים בסעיף ב' והביאו דוגמאות לנקודות כאלו.
    תוכלו להיעזר ביישומון המצורף.

מדרגה 1

מדרגה לסעיף ב':

  •  מצאו נקודה K כך ששטח משולש ABK שווה לחצי משטח משולש ABC.
  • האם יש אפשרויות נוספות לנקודה K?

תוכלו להיעזר ביישומון המצורף.

מדרגה 2

מדרגה לסעיף ב':

  • מצאו נקודה F על הישר AB כך ששטח משולש AFC שווה לחצי משטח משולש ABC.
  • האם יש אפשרויות נוספות לנקודה F?

תוכלו להיעזר ביישומון המצורף.

יישומון למשימה

  • סמנו את שיעורי הנקודות D, E, F: השלימו את שיעור x ואת שיעור y. לחצו Enter.
  • כשהנקודות D, E, F מופיעות במערכת הצירים, לחצו על הכפתור "משולש" ליצירת משולש DEF.
  • ניתן לגרור את הנקודות D, E, F ולשנות את שיעוריהן. שטח המשולש DEF מתעדכן בהתאם.

יישומון למדרגה 1

  • סמנו את שיעורי הנקודה K: השלימו את שיעור x ואת שיעור y. לחצו Enter.
  • כשהנקודה K מופיעה במערכת הצירים, לחצו על הכפתור "משולש" ליצירת משולש ABK.
  • ניתן לגרור את הנקודה K ולשנות את שיעוריה. שטח המשולש ABK מתעדכן בהתאם.

יישומון למדרגה 2

  • סמנו את שיעורי הנקודה F: השלימו את שיעור x ואת שיעור y. לחצו Enter.
  • כשהנקודה F מופיעה במערכת הצירים, לחצו על הכפתור "משולש" ליצירת משולש AFC.
  • ניתן לגרור את הנקודה F ולשנות את שיעוריה. שטח המשולש AFC מתעדכן בהתאם.

הנחיות למורה

כיתה מומלצת

  • כיתה ח', שליש שלישי.

סוג המשימה

  • ריבוי תשובות.
  • פתרון בדרכים שונות.
  • משימה המקשרת בין גאומטריה לאלגברה.

הידע הדרוש

  • סימון נקודות במערכת צירים.
  • חישוב שטח של משולש.
  • חישוב אורכי קטעים במערכת צירים המקבילים לצירים.

מה נלמד

  • מאפיינים של משולשים בעלי יחס מסוים בין שטחיהם.

הדגשים ומטרות

  • התמודדות עם שאלות בעלות תשובות רבות וניתוחן, כשמתחילים עם מקרה פרטי ועוברים להכללה.

דירוג אתגר מתמטי

  • הפניה לאפשרות להיעזר ביישומונים.

מערך דידקטי מומלץ

  • פתיחת השיעור: הצגת המשימה והנדרש בה.
  • עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות).
  • דיונים כיתתיים:
    • התלמידים יציגו את תשובותיהם ואת הדרכים השונות לפתרון לסעיף א'.
    • תלמידים מציגים את תשובותיהם לסעיף ב'.
    • דיון בסעיף ג' והגעה להכללה.

הצעות לפתרונות:

סעיף א'

שטח המשולש הוא 12 יחידות שטח.

סעיפים ב' ו- ג'

חלק מהאפשרויות:

תאור חלק מהאפשרויות:

אורך צלע של המשולש המבוקש הנמצאת על הישר AB:

מיקום הקודקוד השלישי יכול להיות על אחד משני ישרים מקבילים לצלע AB הנמצאים ממנה במרחק: \(h_1\) (גובה המשולש הנתון)

דוגמאות

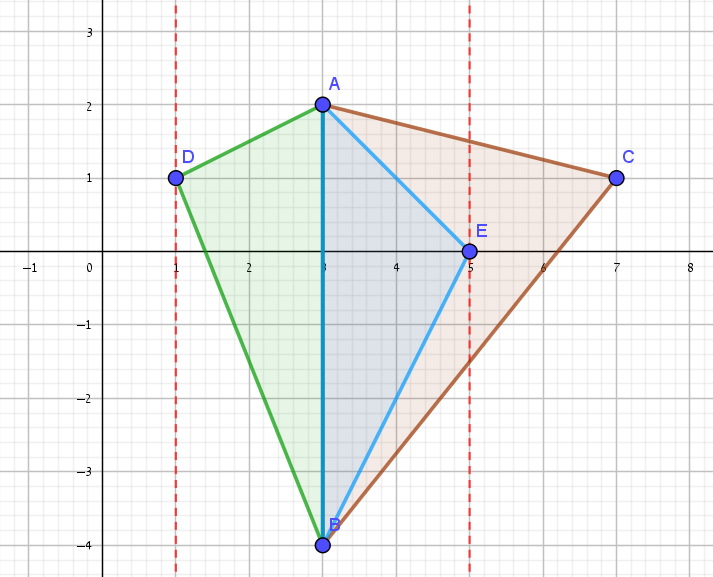
א.

צלע המונחת על הישר AB תהיה שווה באורכה לצלע AB, וגובה המשולש יהיה חצי מגובה המשולש ABC, כלומר הקודקוד השלישי יכול להיות על אחד משני ישרים המקבילים לישר AB ובמרחק חצי מגובה המשולש ABC.

\(AB\)

\(0.5h_1\)

ב.

צלע המונחת על הישר AB תהיה שווה לחצי מאורך הצלע AB, וגובה המשולש יהיה שווה לגובה המשולש ABC, כלומר הקודקוד השלישי יכול להיות על אחד משני ישרים המקבילים לישר AB ובמרחק השווה לגובה המשולש ABC.

\(0.5AB\)

\(h_1\)

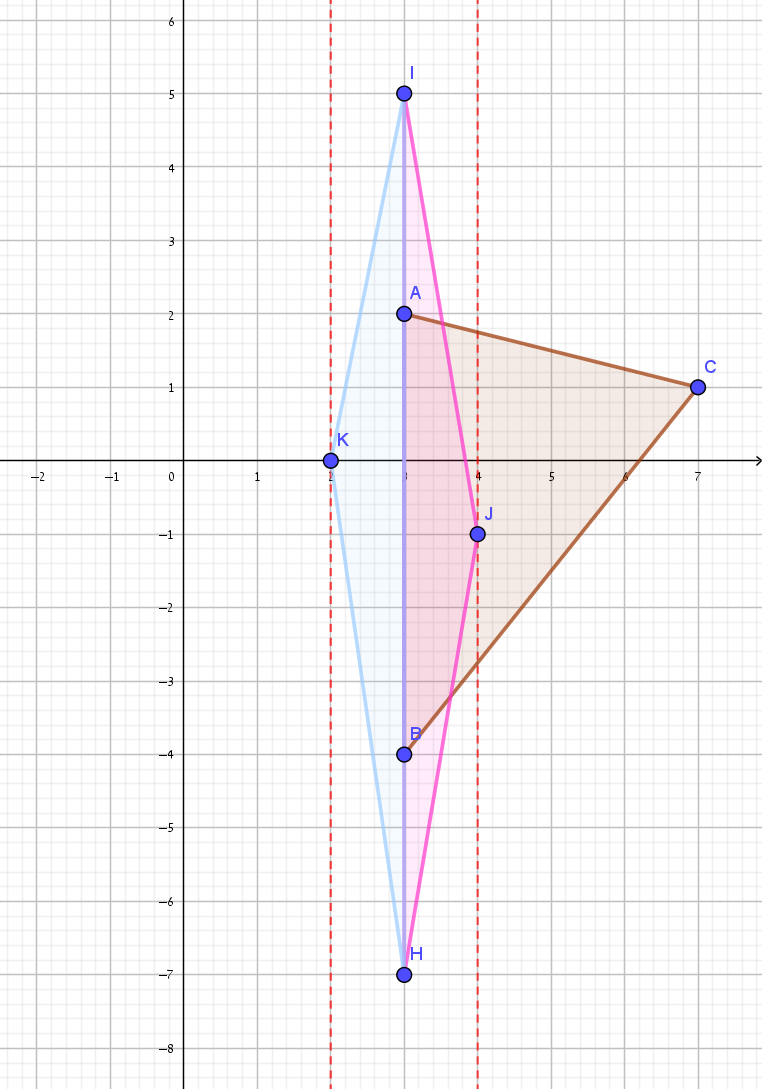
ג.

צלע המונחת על הישר AB תהיה גדולה פי 2 מאורך הצלע AB, וגובה המשולש יהיה רבע מגובה המשולש ABC, כלומר הקודקוד השלישי יכול להיות על אחד משני ישרים המקבילים לישר AB ובמרחק רבע מגובה המשולש ABC.

\(2AB\)

\(0.25h_1\)

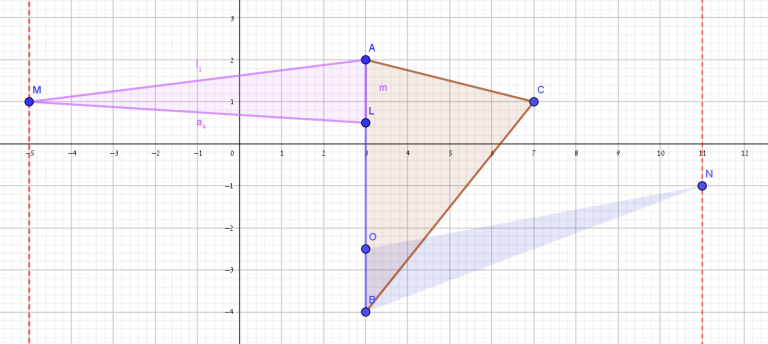
ד.

צלע המונחת על הישר AB תהיה שווה לרבע מאורך הצלע AB, וגובה המשולש יהיה גדול פי 2 מגובה המשולש ABC, כלומר הקודקוד השלישי יכול להיות על אחד משני ישרים המקבילים לישר AB ובמרחק שהוא כפליים מגובה המשולש ABC.

\(0.25AB\)

\(2h_1\)

ה.

ובאופן כללי: אם אורך הצלע המונחת על הישר AB אורכה שווה ל: \(k\cdot AB\space,\space k>0\) אז אורך גובה המשולש ABC היוצא מקודקוד C יהיה מוכפל ב- \(\large\frac{1}{2k}\). כלומר הקודקוד השלישי יכול להיות על אחד משני ישרים המקבילים לישר AB ובמרחק שהוא \(\large\frac{1}{2k}\) מגובה המשולש ABC היוצא מקודקוד C.

\(k\cdot AB\)

\(k>0\)

\(\large\frac{1}{2k}\cdot\normalsize h_1\)

הערה:

שימו לב שהקודקודים של המשולש שנוצר, שנמצאים על הישר העובר דרך נקודות A ו- B, לא חייבים להימצא על הצלע AB.