מגן דוד - למורה
משימה
הסרטוט שלפניכם נוצר משני משולשים שווי צלעות.
אורך כל צלע של אחד מהמשולשים הוא 8 ס"מ, ושל השני 9 ס"מ.
המשולשים הונחו זה על גבי זה כך ש: \(DE∥AB\).
- מה ניתן לאמר על ששה המשולשים הקטנים שבסרטוט?
הסבירו. - מצאו מהו היקף המשושה שנוצר?
פתרו בכמה שיותר דרכים.
- ניתן לגרור כל אחד מהמשולשים, על ידי גרירה של ה + המתאים.
- ניתן להציג נקודות חיתוך בין הקטעים.
מדרגה 1
תוכלו להיעזר ביישומון המצורף.
- ניתן לגרור כל אחד מהמשולשים, על ידי גרירה של ה + המתאים.
- ניתן להציג נקודות חיתוך בין הקטעים.
- ניתן להציג זוויות מתחלפות.
מדרגה 2
תוכלו להיעזר ביישומון המצורף.
- ניתן לגרור כל אחד מהמשולשים, על ידי גרירה של ה + המתאים.
- ניתן להציג נקודות חיתוך בין הקטעים.
- ניתן להציג זוויות מתחלפות.
- ניתן להציג אורכי צלעות שוות.
הנחיות למורה
כיתה מומלצת
- כיתה ז', שליש שלישי.
סוג המשימה
- ריבוי דרכי פתרון.
- קשר בין תחומים שונים במתמטיקה.
הידע הדרוש
- משולש שווה צלעות.
- זוויות בין ישרים מקבילים.
- היקף מצולעים.
- תובנה אלגברית.
מה נלמד
- חוקיות.
- הכללה של תופעות מספריות.
הדגשים ומטרות
- פיתוח יכולת התלמידים לזהות אורכים שווים של קטעים (צלע משושה כצלע במש"צ).
- פיתוח יכולת התלמידים לפתור מערכות משוואות מרובות משתנים על-ידי שימוש בפעולות אלגבריות פשוטות, ללא צורך בידיעת פתרון מערכת משוואות.
- פיתוח יכולת התלמידים לראות מצולע המורכב ממצולעים שונים (מגן דוד המורכב ממשולשים שווי-צלעות שונים ומשושה).
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות).
- דיונים כיתתיים: התלמידים יציגו את תשובותיהם ואת הדרכים השונות לפתרון.
- כל דרך נכונה ותשובה נכונה מתקבלים.
הצעות לפתרונות:
סעיף א'
כל המשולשים שווי צלעות.
סעיף ב'
דרך א'
אפשרות לסרטוט:
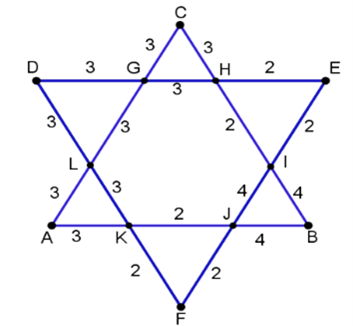
מכאן נקבל שהיקף המשושה המרכזי: \(3+3+2+4+2+3=17\)
אפשרויות נוספות:
- \(2.5,\space3.5,\space2,\space3.5,\space2.5,\space3\)
- \(1,\space3,\space4,\space2,\space2,\space5\)
- \(1.5,\space4,\space3.5,\space0.5,\space5,\space2.5\)
- \(3,\space4.5,\space0.5,\space4,\space3.5,\space1.5\)
דרך ב'

\(x+b+r=8 \space\space\space\space;\space\space\space\space r+m+z=8 \space\space\space\space;\space\space\space\space z+y+x=8\)
\(y+z+m=9 \space\space\space\space;\space\space\space\space b+r+m=9 \space\space\space\space;\space\space\space\space b+x+y=9\)
\(3x+3b+3r+3m+3z+3y=51\)
נחלק את המשוואה ב – 3
\(x+b+r+m+z+y=17\)
דרך ג'
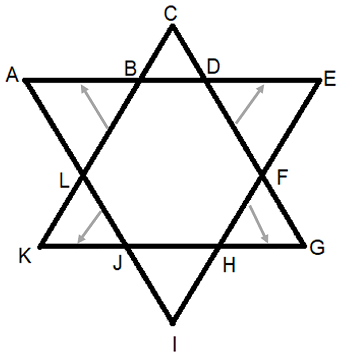
צלעות \(LJ=KJ \space\space\space\space;\space\space\space\space FH=GH \space\space\space\space;\space\space\space\space FD=ED \space\space\space\space;\space\space\space\space LB=AB\)
לכן, היקף המשושה שווה לאורך הצלעות הגדולות האופקיות:
\(GK+AE=8+9=17\)
דרך ד'
נסמן אורך צלע של כל משולש קטן כ: \(a,\space b,\space c,\space d,\space e,\space f\)
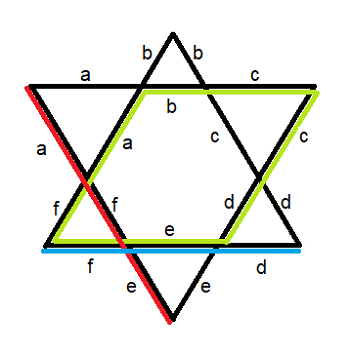
כך, היקף המשושה הוא \(a+b+c+d+e+f\)
\(a+f+e=9\) צלע המשולש
\(b+c=e+f\) צלעות נגדיות שוות במקבילית
\(e+f+d=8\) צלע משולש שני
אז:
\(a+b+c+d+e+f=a+f+e+b+c+d=9+b+c+d=9+e+f+d=8+9=17\)
דרך ה'
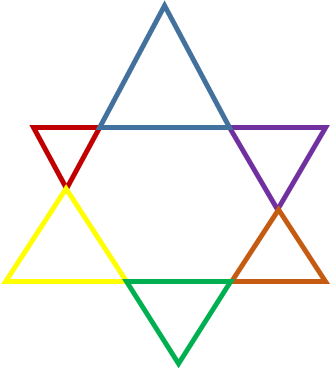
סגול+כחול+אדום=8
צהוב+ירוק+כתום=9
ומכאן, היקף המשושה: 8+9=17


















