סוגי משולשים א - למורה
משימה
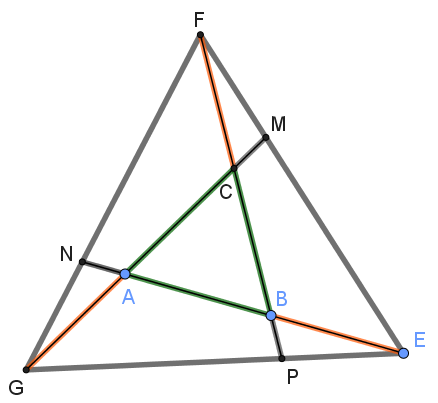
נתון כי משולש ABC הוא משולש שווה צלעות.
המשיכו את צלעות המשולש, כך ש- CF=BE=AG.
חיברו את נקודות E, F ו- G.
נקודות P, N ו- M הן נקודות החיתוך בין צלעות משולש GFE, לבין המשכי הקטעים AE, FB ו- GC בהתאמה (ראו סרטוט מצורף ביישומון).
- מצאו כמה משולשים ישנם בסרטוט המצורף.
- מיינו בדרכים שונות את המשולשים שבסרטוט.
- אילו ערכים יכולה לקבל זווית EFP? נמקו תשובתכם.
משולש
- ניתן להזיז את הנקודות הכחולות: A, B, E ולשנות בהתאם את מידות המשולש.
- ניתן להציג את זווית EFP.
טבלת מיון
- כתבו בתיבה המתאימה שבראש העמודה את שם הקריטריון למיון.
- היעזרו במקש 'ABC' שבסרגל הכלים של היישומון וכתבו את שם המשולש (לדוגמה ABC). לאחר מכן, ניתן לגרור את שם המשולש לעמודה המתאימה בטבלה.
מדרגה
סעיף ב' / ג'
- מצאו בסרטוט קטעים שווי אורך.
- מצאו בסרטוט זוויות שוות.
משולש
- ניתן להזיז את הנקודות הכחולות: A, B, E ולשנות בהתאם את מידות המשולש.
- ניתן להציג את זווית EFP.
- למדידת זווית במשולש, לחצו בסרגל הכלים שלמעלה על הסמל של הזווית
בעזרת העכבר סמנו 3 נקודות עם כיוון השעון. גודל הזווית שאת קודקודיה סימנתם – יוצג. - למדידת אורך קטע, לחצו בסרגל הכלים שלמעלה על הסמל של מדידת אורך קטע
בעזרת העכבר סמנו 2 נקודות, שהן קצות הקטע הרצוי. אורך הקטע שאת קצותיו סימנתם – יוצג.
טבלת מיון
- כתבו בתיבה המתאימה שבראש העמודה את שם הקריטריון למיון.
- היעזרו במקש 'ABC' שבסרגל הכלים של היישומון וכתבו את שם המשולש (לדוגמה ABC). לאחר מכן, ניתן לגרור את שם המשולש לעמודה המתאימה בטבלה.
הנחיות למורה
כיתה מומלצת
- כיתה ח', שליש שלישי
סוג המשימה
- ניתוח נתוני השאלה והסקת מסקנות.
- מיון משולשים בדרכים שונות.
הידע הדרוש
- חפיפת משולשים.
- דמיון משולשים על פי זוויות.
- מול הצלע הגדולה במשולש מונחת הזווית הגדולה.
מה נלמד
- העמקה וחידוד בנושא חפיפת משולשים.
- הבנה וחידוד בנושא דמיון משולשים.
הדגשים ומטרות
- השוואה בין חפיפה לדמיון משולשים וניתוחן.
דירוג אתגר מתמטי
- הכוונה לפתרון.
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- אירגון הכתה: ניתן לארגן את השיעור בצורה של תחרות קבוצתית באופן הבא: לחלק את הכתה לקבוצות של 4 תלמידים. כל אחת מהקבוצות תפתור את המשימה כולה. בסיום העבודה כל קבוצה מגישה למורה את פתרון כל סעיפי השאלה.
- דיון כיתתי:
- בתחילה כל קבוצה תדווח כמה משולשים היא מצאה.
- בשלב הבא נציג מכל כל קבוצה ידווח על קטגוריה אחת למיון שהקבוצה מצאה.
- לאחר מכן נציג מכל קבוצה ידווח על זוג אחד (או שלשה אחת) של משולשים חופפים שהקבוצה מצאה או על זוג משולשים דומים וינמק.
- ובהמשך נציג מכל קבוצה ידווח על שיוך משולשים לקטגוריות נוספות.
- המורה יקבע מי הקבוצה המנצחת בהתאם לתשובות שהקבוצות מסרו.
הצעות לפתרונות:
פתרון המשימה:
- ישנם 17 משולשים.
- הצעות למיונים מופיעות בטבלאות בהמשך.
- גודלה של זווית EFP יכול להיות בין 0° ל 30°
הצעות למיונים:
| קשרים בין משולשים | חופפים | דומים שאינם חופפים |
|---|---|---|
| המשולשים | \(\triangle FCM\cong \triangle EBP\cong \triangle GAN\) \(\triangle FBE\cong \triangle GCF\cong \triangle EAG\) \(\triangle MAE\cong \triangle NBF\cong \triangle PCG\) \(\triangle FPE\cong \triangle ENG\cong \triangle GMF\) \(\triangle FGP\cong \triangle EFN\cong \triangle GEM\) | \(\triangle ABC \sim \triangle GFE\) |
| מספר הזוויות בנות \(60^{\circ}\) במשולש | משולשים בעלי זווית אחת בת \(60^{\circ}\) | משולשים בעלי שלוש זוויות בנות \(60^{\circ}\) | משולשים ללא זווית בת \(60^{\circ}\) |
|---|---|---|---|
| המשולשים | \(\triangle FPE\) \(\triangle NEG\) \(\triangle FMG\) \(\triangle FCM\) \(\triangle PBE\) \(\triangle GNA\) \(\triangle MAE\) \(\triangle NBF\) \(\triangle PCG\) \(\triangle FEN\) \(\triangle FGP\) \(\triangle GEM\) | \(\triangle ABC\) \(\triangle GFE\) | \(\triangle FBE\) \(\triangle GAE\) \(\triangle FCG\) |
| לפי סוגי הזויות | חד זווית | ישר זווית | קהה זווית |
|---|---|---|---|
| \(\triangle ABC\) \(\triangle GFE\) \(\triangle FEN\) \(\triangle FGP\) \(\triangle GEM\) \(\triangle MAE\) \(\triangle NBF\) \(\triangle PCG\) | \(\triangle FBE\) \(\triangle GAE\) \(\triangle FCG\) \(\triangle FCM\) \(\triangle PBE\) \(\triangle GNA\) \(\triangle FPE\) \(\triangle NEG\) \(\triangle FMG\) |