הנחיות למורה

כיתה מומלצת

• כיתה ח', שליש שלישי.

סוג המשימה

• ריבוי תשובות בטווח מסויים.
• פתרון בדרכים שונות.

הידע הדרוש

• פתרון בעיות דרך.
• גרף של פונקציה קווית.
• סרטוט גרף בתחומים שונים.

מה נלמד

• העמקה בפתרון בעיות דרך.

הדגשים ומטרות

• התמודדות עם שאלות בעלות תשובות רבות וניתוחן, כלומר יש אין סוף תשובות נכונות, אבל במגבלות מסוימות.
• אפשרויות פתרון בדרכים שונות: בדיקת מקרים פרטיים, פתרון אי שוויונות, פתרון בעזרת איור, פתרון גרפי.

דירוג אתגר מתמטי

• הפניה לבדיקת מקרים פרטיים.
• הפניה לאפשרות להיעזר ביישומון.

מערך דידקטי מומלץ

• פתיחת השיעור: הצגת המשימה והנדרש בה.
• עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות).
• דיונים כיתתיים: התלמידים יציגו את תשובותיהם ואת הדרכים השונות לפתרון.
• כל דרך נכונה ותשובה נכונה מתקבלים.

הצעות לפתרונות:

דרך פתרון א'

מקרה א':

המכונית משיגה את האופנוע לפני המנוחה:

על המכונית לעבור 75 ק"מ ב- פחות משעה, כלומר מהירותה צריכה להיות גדולה מ- 75 קמ"ש, אבל גם קטנה מ- 100 קמ"ש בגלל מגבלות החוק \((75<V≤100)\).

מקרה ב':

המכונית משיגה את האופנוע בזמן המנוחה:

אם הם נפגשים בשעה 11:30, כלומר בתחילת המנוחה, על המכונית לעבור 75 ק"מ במשך שעה, כלומר מהירותה 75 קמ"ש.

אם הם נפגשים בשעה 11:45, כלומר בסוף המנוחה, על המכונית לעבור 75 ק"מ במשך שעה ורבע, כלומר מהירותה 60 קמ"ש.

לכן מהירות המכונית יכולה להיות בין 60 קמ"ש ל 75 קמ"ש \((60≤V≤75)\).

מקרה ג':

המכונית משיגה את האופנוע לאחר המנוחה ולפני ההגעה לרחובות:

האופנוע מגיע לרחובות לאחר שנסע שעה מסיום המנוחה במהירות 51 קמ"ש.

המכונית צריכה לפגוש את האופנוע לאחר שנסעה פחות משעתיים ורבע לכן מהירותה צריכה להיות גדולה מ- 56 קמ"ש \((126∶(1.5+0.25+1-0.5)=56)\), אבל מהירותה צריכה להיות קטנה מ- 60 קמ"ש כדי שהם יפגשו לאחר המנוחה \((56<V<60)\).

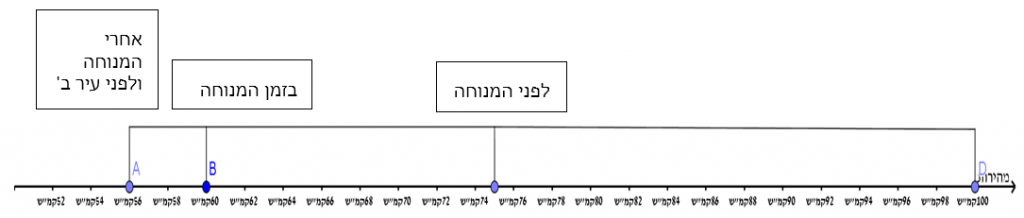
דרך פתרון ב'

פתרון גרפי למשימה – ניתן להראות בעזרת היישומון המצורף.

סרטוט סכמתי של מהירויות המכונית: