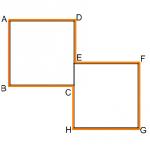
יצירת מתומן משני ריבועים - למורה
משימה
- צרו מתומן משני ריבועים. תארו כיצד יצרתם אותו.
- צרו משני ריבועים מתומן אחר. תארו מה ההבדל בין שני המתומנים.
- צרו מתומנים נוספים משני ריבועים.
מדרגה
- האם הריבועים זהים? שונים?
- איזה סוגי מתומנים התקבלו? משוכללים או לא?
- כמה קודקודים צריכים להיות על מנת לבנות מתומן כנדרש?
ניתן להיעזר ביישומון.
- ניתן לשנות את אורך הצלע של כל ריבוע בעזרת סרגל הגרירה המתאים.
- ניתן לגרור ("הזזה") ולסובב ("סיבוב") כל אחד מהריבועים בעזרת ה"ידיות" המחוברות אליהם.
הנחיות למורה
כיתה מומלצת
- כיתה ז'.
סוג המשימה
- משימה פתוחה המאפשרת לשאול שאלות שונות.
- תשובות שונות.
- מדוגמאות להכללה.
הידע הדרוש
- מספר הקודקודים / הצלעות הנדרש ליצירת המתומן.
- הכרת מצולעים שאינם משוכללים.
מה נלמד
- תכונות בסיסיות של מתומן.
הדגשים ומטרות
- שבירת האב-טיפוס של המושג מתומן שמכיל תכונות אי קריטיות רבות (שוויון של זוויות וצלעות) והתייחסות למושג הרחב של מתומן ולא לתת קטגוריה שלו (מתומן משוכלל).
״אנליזה של מושג פירושה לנתח את המושג ולבחון את תכונותיו הקריטיות היסודיות (8 צלעות). תכונות אלו חייבות להיות באובייקט שהוא דוגמה של המושג. ואילו תכונות אי קריטיות יכולות להשתנות מדוגמה לדוגמה״ (הרשקוביץ, 1989). - התאמה בין מספר הצלעות של מצולע למספר קודקודיו.
- יצירת מתומנים שונים בעזרת אותם ריבועים.
אפיון המשימה
- משימה חקר.
- הסקת מסקנות.
- ניסוח תכונות של מתומן כמקרה פרטי של מצולע.
מערך דידקטי מומלץ
- עבודה עצמית של התלמידים ביחידים.
- דיון בקבוצות: תכונות משותפות לכל המתומנים שנבנו (8 צלעות, 8 קודקודים, 8 זוויות), תכונות שונות (אורכים שונים של צלעות, זוויות שונות, למעט הזוויות הישרות שנשמרות)
- סיכום – מה מאפיין את המתומנים שנוצרו (שבירת צלעות תוך שימור מספר הקודקודים הסופי). מה התכונות הקריטיות שחייבות להישמר לעומת תכונות אי קריטיות.
הצעות לפתרונות:
להלן אפשרויות למתומנים: