התאמת ביטויים לגרפים של פרבולות - חלק א - למורה
משימה
סעיף א
- כתבו ביטויים מתאימים ל-4 הפרבולות שבתמונה (הפרבולות חופפות).
- מצאו לפחות עוד שתי אפשרויות לביטויים מתאימים.

מדרגה לסעיף א
לכל אחד מהסרטוטים הבאים רשמו ביטויים לפרבולות שהגרפים שלהן נתונים בסרטוט (הפרבולות חופפות):

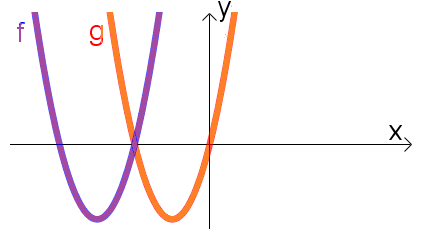
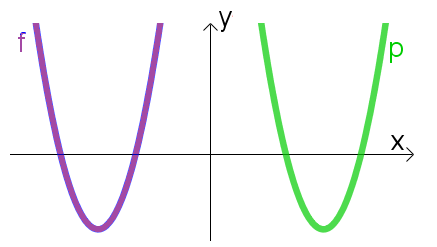
- הקלידו בתיבות, ביטויים של פונקציות המתאימות לפרבולות שבתמונה.
- לקבלת משוב לחצו על הכפתור בדיקה.
- המשוב מתייחס גם לכל פונקציה בנפרד וגם לקשר ביניהן:
- הצבע שבו יופיע השם של כל פונקציה במשוב:
כחול – ביטוי אפשרי; אדום – ביטוי שגוי. - צבעי הקטעים המחברים בין שמות הפונקציות השונות:
חיבור כחול – שתי הפונקציות יחד מתאימות לתמונה;
חיבור אדום – הצירוף של שתי הפונקציות יחד לא מתאים לתמונה. - לאחר שינוי של ביטוי באחת הפונקציות – לחצו שוב על כפתור הבדיקה.
- הצבע שבו יופיע השם של כל פונקציה במשוב:
סעיף ב
- כתבו ביטויים מתאימים ל-4 הפרבולות שבתמונה (הפרבולות חופפות).
- מצאו לפחות עוד שתי אפשרויות לביטויים מתאימים.
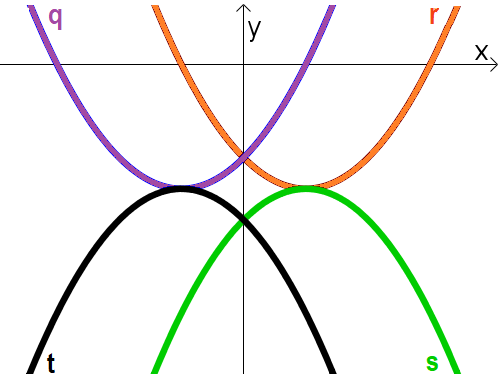
מדרגה לסעיף ב
לכל אחד מהסרטוטים הבאים רשמו ביטויים לפרבולות שהגרפים שלהן נתונים בסרטוט (הפרבולות חופפות):
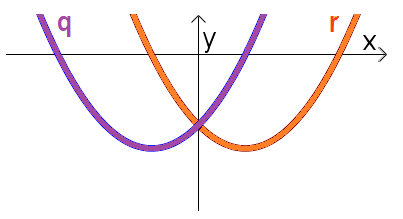
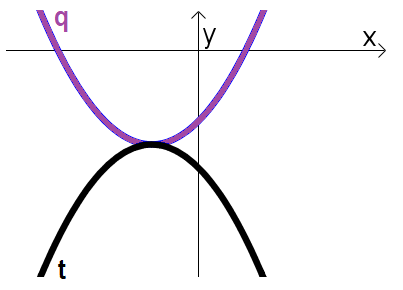

- הקלידו בתיבות, ביטויים של פונקציות המתאימות לפרבולות שבתמונה.
- לקבלת משוב לחצו על הכפתור בדיקה.
- המשוב מתייחס גם לכל פונקציה בנפרד וגם לקשר ביניהן:
- הצבע שבו יופיע השם של כל פונקציה במשוב:
כחול – ביטוי אפשרי; אדום – ביטוי שגוי. - צבעי הקטעים המחברים בין שמות הפונקציות השונות:
חיבור כחול – שתי הפונקציות יחד מתאימות לתמונה;
חיבור אדום – הצירוף של שתי הפונקציות יחד לא מתאים לתמונה. - לאחר שינוי של ביטוי באחת הפונקציות – לחצו שוב על כפתור הבדיקה.
- הצבע שבו יופיע השם של כל פונקציה במשוב:
הנחיות למורה
כיתה מומלצת
- כיתה ט', שליש שלישי.
סוג המשימה
- משימה פתוחה.
- ריבוי תשובות.
- דרכים שונות.
הידע הדרוש
- תכונות של גרף הפונקציה הריבועית.
- ייצוגים שונים של הפונקציה הריבועית.
- קשרים בין משוואת הפרבולה לגרף הפרבולה.
- טרנספורמציות של הפונקציה הריבועית בייצוגיה השונים.
מה נלמד
- העמקה וחידוד ההבנה של תכונות של פונקציה ריבועית.
הדגשים ומטרות
- פיתוח היכולת לזהות תכונות של הפונקציה הריבועית על פי הגרף שלה.
- פיתוח היכולת לזהות מצבים הדדיים בין הגרפים של פונקציה ריבועית.
- פיתוח היכולת למצוא משוואת פרבולה על פי מאפייני הגרף שלה.
- פיתוח היכולת לבחור בייצוג המתאים ובטרנספורמציה מתאימה כדי למצוא את משוואת הפרבולה המתאימה לגרף נתון.
דירוג אתגר מתמטי
- כל סעיף במשימה המקורית (בה ישנם ארבעה גרפים) מחולק לכמה שאלות פשוטות יותר שבהן ישנם רק שני גרפים.
מערך דידקטי מומלץ
אפשרויות שונות לאירגון השיעור:
- אפשרות א': כל התלמידים (בקבוצות) פותרים את שני הסעיפים.
- אפשרות ב': חלק מקבוצות התלמידים פותרים את סעיף א', החלק השני של הקבוצות פותר את סעיף ב'. בדיון הכיתתי דנים ומסבירים את שני הסעיפים, וכשיעורי בית התלמידים משלימים את הסעיף שלא פתרו בכיתה.
- אפשרות ג': חלק מקבוצות התלמידים פותרים את סעיף א', החלק השני של הקבוצות פותר את סעיף ב'. ואח"כ מערבבים בין תלמידי הקבוצות – ויוצרים "למידת עמיתים".
- אפשרות ד': את אחד הסעיפים פותרים בכיתה ואת הסעיף השני פותרים כשיעורי בית, ודנים בו בשיעור שלאחר מכן.
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (בקבוצות). רצוי שתלמידים יעזרו ביישומון המצורף.
תלמידים יבחרו אם להיעזר במדרגות. - דיונים כיתתיים:
דיון בכל סעיף במשימה:- נציג מכל אחת מהקבוצות יציג את הביטויים שהקבוצה מצאה לגרפים באותו סעיף ויסביר כיצד הקבוצה הגיעה לתשובותיה.
- יתקיים דיון כיתתי לגבי השאלות:
א. האם התשובות נכונות? אם לא – מה יש לתקן? וכיצד? רצוי להציג את הגרפים המתקבלים מתשובות התלמידים בעזרת תוכנה המאפשרת סרטוט גרפים.
ב. לפי אילו עקרונות ניתן להגיע לביטויים המתאימים לגרפים הנתונים באותו סעיף.
הנחיות למורה
תלמידים אינם נדרשים להציג את תשובותיהם ולהסבירם בעזרת פרמטרים. ניתן להסביר את הקשרים בין הפרמטרים בביטויים של הפרבולות במילים.
כל דרך נכונה לפתרון מתקבלת, וכל תשובה נכונה מתקבלת.
הצעות לפתרונות:
- \(f(x)=a(x+2d)(x+d)\space\space , \space\space g(x)=ax(x+d)\space\space , \space\space h(x)=ax(x-d)\space\space ,\space\space p(x)=a(x-2d)(x-d)\)
כאשר: \(a>0\space\space , \space\space d>0\)
\(\space\) - \(q(x)=a(x+d)(x-e)\space\space , \space\space r(x)=a(x-d)(x+e)\)
ניתן לחשב את שיעורי הקודקוד \((x_m,y_m)\) של \(q(x)\) ואז:
\(t(x)= -a(-x-x_m )^2+y_m \space\space , \space\space s(x)= -a(x-x_m )^2+y_m\)
כל זה כאשר: \(a>0 \space\space , \space\space d>0 \space\space , \space\space e>0 \space\space , \space\space d>e\)
ניתן להתחיל מייצוג קודקודי, אך יש לדאוג שנקודת החיתוך עם ציר y תהיה שלילית.


















