מרחק מבית הספר - למורה
משימה
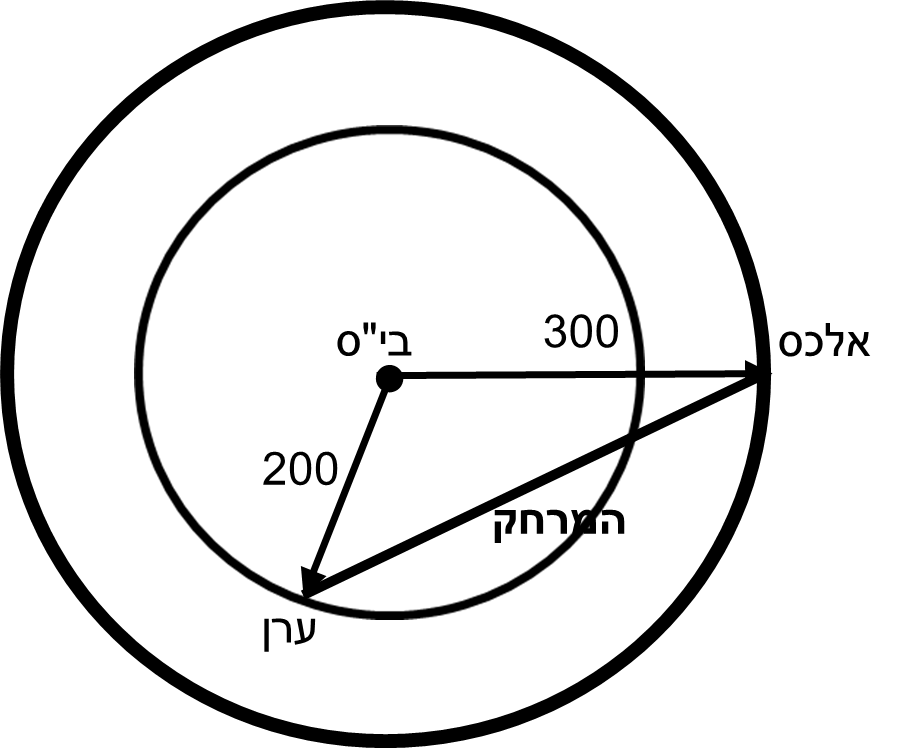
ביתו של ערן נמצא במרחק 200 מטר מבית הספר, וביתו של אלכס נמצא במרחק 300 מטר מביה״ס.
מהו המרחק בין הבתים של ערן ואלכס?
סמנו את המרחק בין הבתים של ערן ואלכס ב- \(S\) ורשמו את התשובה בעזרת \(S\).
מדרגה
- ניתן להיעזר ביישומון.
- ניתן לגרור את הנקודות המסמלות את ביתו של ערן ואת ביתו של אלכס.
- ניתן לגרור את הנקודה המסמלת את ביתו של אלכס.
הנחיות למורה
כיתה מומלצת
- כיתה ט'.
סוג המשימה
- משימה בעלת תשובות רבות (אין-סוף תשובות בתחום מסויים).
- הצגות שונות לדרך פתרון (סרטוט האפשרויות השונות של המיקום של ביה״ס והבתים וסימון המרחק ביניהם).
הידע הדרוש
- המשפט: סכום כל שתי צלעות במשולש גדול מהצלע השלישית (או: כל צלע במשולש קטנה מסכום שתי הצלעות האחרות).
- היכרות בסיסית עם מעגל.
מה נלמד
- יישום בחיי יום יום של המשפט לגבי הקשר בין האורכים של צלעות במשולש.
- לקבוצות ברמה גבוהה – התייחסות למעגל כמקום גיאומטרי.
הדגשים ומטרות
- תכונות המעגל: רדיוס, קוטר.
- שני מעגלים בעלי מרכז משותף ודיון – מדוע ביה״ס הוא מרכז של שני המעגלים.
- בחינת המרחקים כאשר נוצרים משולשים, תוך שימוש במשפט הנ״ל.
- התייחסות למרחקים שמתלכדים עם הקוטר והסבר מדוע המשפט אינו תקף במקרה זה.
- ניתן לדעת רק את הטווח של המרחקים האפשריים ולא את המרחק המדויק (למעט בקצוות).
דירוג אתגר מתמטי
- שימוש ביישומון.
מערך דידקטי מומלץ
- עבודה בזוגות או בקבוצות.
- הצגת דרכים שונות לפתרון (תרשים של האפשרויות).
- הצגה של האופן שניתן להגיע לכל המרחקים האפשריים (שני מעגלים בעלי מרכז משותף, שהוא ביה״ס).
פתרונות
\(100≤S≤500\)
מצב א
מרחק מינימלי \(300-200=100\). כאשר יש התלכדות של הקטרים.
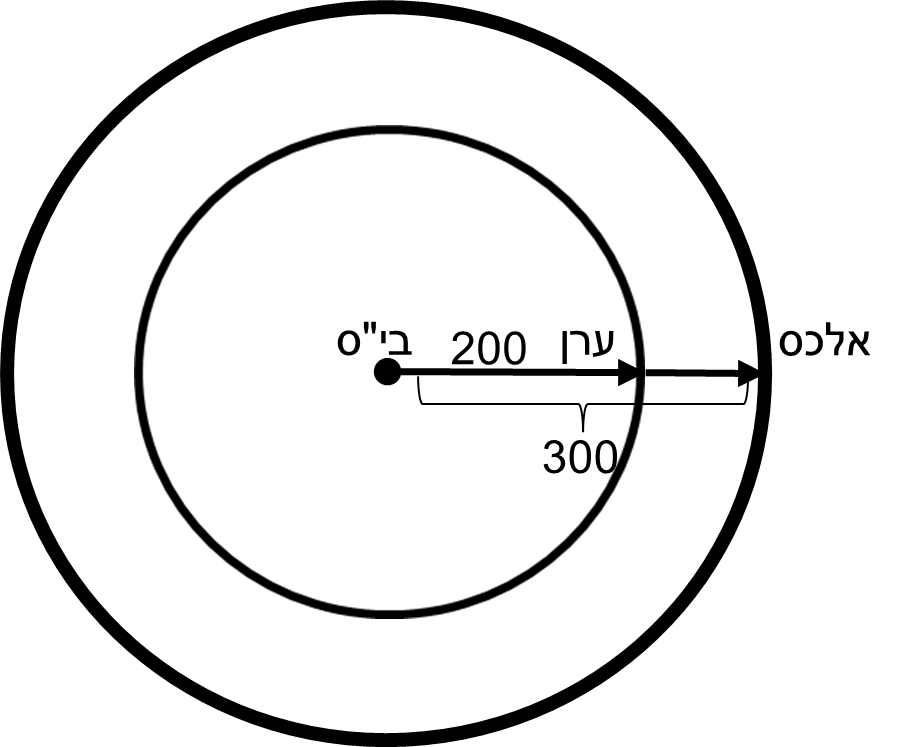
מצב ב
מרחק מקסימלי \(300+200=500\). הזווית בין הקטרים \(180^{\circ}\).

מצב ג
כל צלע במשולש, קטנה מסכום שתי הצלעות האחרות. לכן, המרחק הוא כל מספר בין המרחק המינימלי 100, למרחק המקסימלי 500.