יום עצמאות - למורה
משימה
לקראת חגיגות יום העצמאות מועצת התלמידים של בית הספר תכננה לקנות בלוני הליום ודגלים.
ידוע גם שמחירו של בלון הליום אחד הוא 4 ש״ח ומחירו של דגל אחד הוא 12 ש״ח.
מועצת התלמידים רצתה להכין מארזים לכל אחת מהכיתות בבית הספר.
- המועצה החליטה כי העלות הכוללת של כל מארז תהיה 48 ש״ח. כמה בלונים וכמה דגלים אפשר לקנות?
- המועצה החליטה כי בכל מארז בעלות של 48 ש"ח צריכים להיות לכל היותר 8 פריטים. כמה בלונים וכמה דגלים יכולים להיות במארז כזה?
- המועצה רצתה להוזיל את העלות של כל מארז, כך שעדיין יכיל 8 פריטים ועלותו תהיה נמוכה מ- 48 ש"ח. האם זה אפשרי? אם כן, מהן האפשרויות?
- מה העלות המינימלית האפשרית של מארז עם 8 פריטים?
מדרגה
- תוכלו להיעזר ביישומון
- לסעיף 1 בחרו ב- "סעיף 1"
- לסעיף 2 בחרו ב- "סעיף 2"
- לסעיף 3 בחרו ב- "סעיף 3"
- לסעיף 4 בחרו ב- "סעיף 4"
הנחיות למורה
כיתה מומלצת
- כיתה ח', שליש שני.
סוג המשימה
- אוריינות.
- דרכים שונות לפתרון (חשבוני, גרפי ואלגברי).
- ניתוח דוגמאות והמשמעות שלהן.
הידע הדרוש
- בניית משוואה ממעלה ראשונה.
- פתרון אלגברי וגרפי של מערכת משוואות ממעלה ראשונה.
- קריאת גרף.
מה נלמד
- מעבר מייצוג מילולי לייצוגים אלגבריים וגרפיים.
- המשמעות של זוגות סדורים (שיעורי נקודות).
- הבנת המשמעות של ההתייחסות לנקודות ששיעוריהן מספרים שלמים בלבד.
- משמעות של מיקום נקודות ביחס לישרים: על הישרים, בין הישרים.
הדגשים ומטרות
- קשר בין הייצוגים השונים של פונקציה ממעלה ראשונה.
- היתרון של כל אחד מהייצוגים.
- התאמת התוכן של השאלה לסוג המספרים שיכולים להתקבל כפתרון.
- תוכן השאלה מגביל את מספר האפשרויות.
דירוג אתגר מתמטי
- מדוגמאות למסקנות.
מערך דידקטי מומלץ
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות) על כל סעיפי השאלה. יש לשים לב שסרטוט מדויק של הגרפים מאפשר פתרון מלא של השאלה ללא פתרון אלגברי.
- ניתן גם להגיע לפתרונות בדרך חישובית בלבד (הצבת מספרים שלמים שמתאימים לתנאי השאלה).
- דיון כיתתי: התלמידים יציגו את הפתרונות השונים ויסבירו את משמעותם.
הצעה לפתרון:
סעיף 1:
מסמנים את מספר הבלונים ב- x ואת מספר הדגלים ב- y.
מתקבלת המשוואה הבאה: \(4x+12y=48\).
ניתן להציג זאת באופן גרפי:
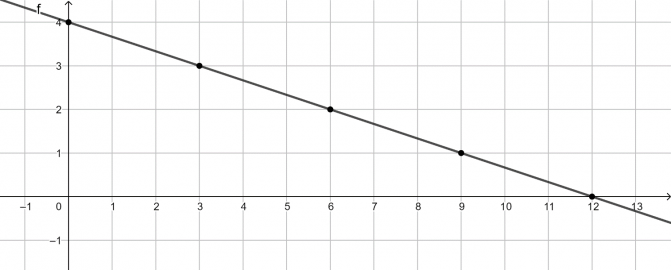
דרך אחרת היא לבדוק מספרית את האפשרויות:
| 12 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | x |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | y |
כלומר מתקבלים הזוגות הסדורים: \((0 ,4)\space\space,\space\space(3 ,3)\space\space,\space\space(6 ,2)\space\space,\space\space(9 ,1)\space\space,\space\space(12 ,0)\).
סעיף 2:
למשוואה מהסעיף הקודם מצטרף אי השוויון: \(x+y ≤8\)
ניתן להציג את מערכת המשוואות באופן גרפי:
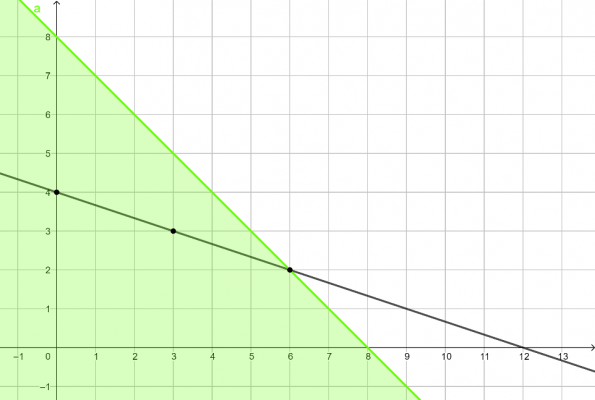
בנוסף, ניתן להסתכל על הזוגות הסדורים שהתקבלו בסעיף א'.
הזוגות שמתאימים הם:
\((0 ,4)\space\space,\space\space(3 ,3)\space\space,\space\space(6 ,2)\).
סעיף 3:
בוחנים את כל האפשרויות למארז שמורכב מ- 8 פריטים.
מסתבר שיש שתי אפשרויות להוזיל את המארז: \((7 ,1)\space\space,\space\space(8 ,0)\).
סעיף 4:
העלות המינימלית מתקבלת כאשר יש במארז רק 8 בלונים ו- 0 דגלים – העלות תהיה אז 32 ש״ח.


















