מחיר חולצה - למורה
משימה
בעל חנות קנה 38 חולצות. הוא מכר 26 חולצות ברווח של 20%.
אילו היה מוכר את 12 החולצות שנותרו בהנחה של 25% ממחיר המכירה הקודם, אז הפדיון הכולל עבור 38 החולצות היה 2,520 ש״ח.
- מה היה המחיר ששילם בעל החנות עבור כל חולצה? הציעו דרכים שונות לפתרון.
- בעל החנות בודק אפשרויות למכור בסוף העונה את 12 החולצות הנותרות בהנחה הגדולה מ- 25% ממחיר המכירה הקודם. הציעו לו דרכים שונות לעשות זאת ועדיין לא להפסיד.
מדרגה
- ניתן להיעזר ביישומון.
- קבעו את אחוז ההנחה האפשרית בסרגל הגרירה.
- ניתן לבחון את המצב המתוכנן מול הביצוע על ידי בחירת התיבה המתאימה.
הנחיות למורה
כיתה מומלצת
- כיתה ח', שליש שני.
סוג המשימה
- פתרון בדרכים שונות.
- לגבי סעיף ב' – משימה פתוחה.
הידע הדרוש
- שליטה באחוזים.
- פתרון של בעיה מילולית.
- פתרון של משוואה ואי-שוויון ממעלה ראשונה.
- שטחים של מלבנים.
מה נלמד
- העמקה בפתרון של בעיה מילולית עם אחוזים.
- ניתוח טווח הערכים האפשריים של הפתרונות.
- דרכי פתרון בייצוגים שונים (פתרון בעזרת תרשים ופתרון אלגברי).
הדגשים ומטרות
- חשיפה לפתרון בדרכים שונות של בעיה מילולית.
- הבנה מעמיקה של המושג ״אחוז״.
- הפיכת שאלה סגורה לשאלה פתוחה.
דירוג אתגר מתמטי
- הפניה לאפשרות להיעזר ביישומון.
מערך דידקטי מומלץ
- עבודה של התלמידים (ביחידים, בזוגות או בקבוצות) על סעיף א.
- דיון כיתתי: חשיפה לדרכים שונות לפתרון. חשוב להציג גם את התרשים שמוביל לפתרון.
- עבודה בקבוצות על סעיף ב׳.
- דיון כיתתי מסכם בו יעלו התלמידים את הצעותיהם.
הצעות לפתרונות:
סעיף א'
נסמן ב- x את מחירה המקורי של החולצה. היות ופדיון משמעותו סך כל ההכנסה ללא ניכויים, אזי ניתן להציג את המשוואה הבאה:
\(26\cdot1.2x+12\cdot0.75\cdot1.2x=2520\)
פתרון המשוואה יביא אותנו לכך שמחיר החולצה בעת הקנייה הוא: \(x=ח"ש\space 60\).
פתרון בעזרת תרשים:
תכנון:
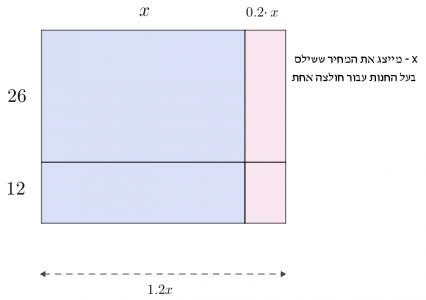
ביצוע:
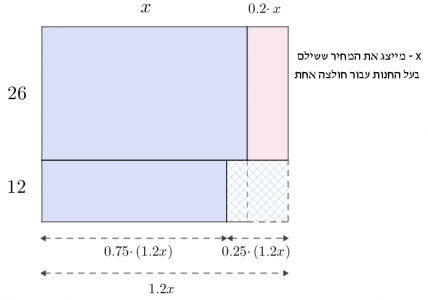
מהתרשים יכולה להתקבל משוואה אחרת:
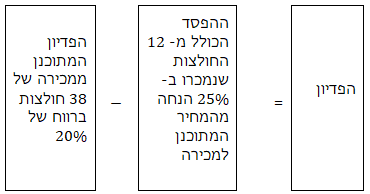
\(38\cdot1.2x- 12\cdot(0.25\cdot1.2)x = 2520\)
\(38\cdot1.2x- 12\cdot0.3x = 2520\)
סעיף ב'
החולצות נקנו ב- 2,280 ש״ח \((38\cdot60=)\).
26 חולצות נמכרו ברווח של 20%, כלומר 72 ש״ח לחולצה, לכן הפדיון ממכירתן הוא 1,872 ש״ח.
כדי להרוויח עליו למכור את 12 החולצות הנותרות לפחות ב- \(2,280-1,872=408\).
לכן, כל חולצה צריכה להימכר במחיר הגדול מ- \(\large\frac{408}{12}\normalsize=ח"ש\space34\).
כלומר, אם מוכרים כל חולצה בהנחה שאינה גדולה מ- 52% (בערך) (ממחיר המכירה, 72 ש"ח) עדיין יישאר בידי הסוחר רווח. כלומר אם d מייצג את אחוז ההנחה אז \(25<d≤52\).
בנוסף, ניתן לחלק את מכירת 12 החולצות הנותרות למחירים שונים כך שסך הפדיון יעלה על 408 ש״ח.


















