שלוש נקודות - חלק א - למורה
משימה
נתונות שלוש נקודות: \(A(-2,-3)\space\space,\space\space B(5,-3)\space\space,\space\space C(2,1)\)
- מצאו בדרכים שונות את שטח משולש ABC.
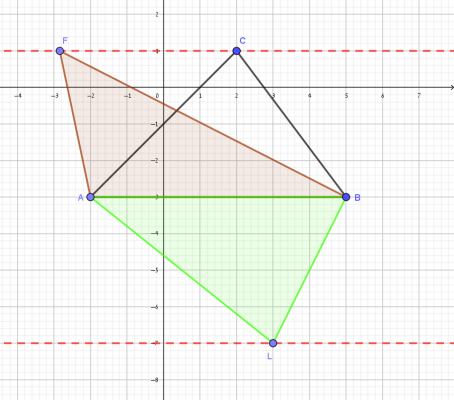
- מצאו נקודה F כך ש: \(S_{ABC}=S_{ABF}\)
- האם התשובה לסעיף ב' היא תשובה יחידה? נמקו תשובתכם.
מדרגות
- ניתן להיעזר ביישומון המצורף.
- סמנו את שיעורי הנקודה F: השלימו את שיעור x ואת שיעור y. לחצו Enter.
- כשהנקודה F מופיעה במערכת הצירים, ניתן לגרור אותה ולשנות את שיעוריה. שטח המשולש ABF מתעדכן בהתאם.
- סמנו את שיעורי הנקודה F: השלימו את שיעור x ואת שיעור y. לחצו Enter.
- כשהנקודה F מופיעה במערכת הצירים, ניתן לגרור אותה ולשנות את שיעוריה. שטח המשולש ABF מתעדכן בהתאם.
הנחיות למורה
כיתה מומלצת
- כיתה ח', שליש שלישי.
סוג המשימה
- ריבוי תשובות.
- פתרון בדרכים שונות.
- משימה המקשרת בין גאומטריה לאלגברה.
הידע הדרוש
- סימון נקודות במערכת צירים.
- חישוב שטח של משולש.
- חישוב אורכי קטעים במערכת צירים המקבילים לצירים.
מה נלמד
- מה מאפיין משולשים בעלי צלע משותפת ושטח שווה.
הדגשים ומטרות
- התמודדות עם שאלות בעלות תשובות רבות וניתוחן, כשמתחילים עם מקרה פרטי ועוברים להכללה.
- מציאת דרכים שונות למציאת שטח משולש ששיעורי קודקודיו נתונים.
דירוג אתגר מתמטי
- הפניה לאפשרות להיעזר ביישומונים.
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות).
- דיונים כיתתיים:
- התלמידים יציגו את תשובותיהם ואת הדרכים השונות לפתרון לסעיף א'.
- תלמידים מציגים את תשובותיהם לסעיף ב'.
- דיון בסעיף ג' והגעה להכללה.
הצעות לפתרונות:
סעיף א'
שטח המשולש הוא 14 יחידות שטח.
הצעות לדרכי פתרון:
דרך א
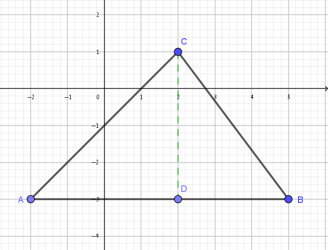
\(D(2,-3)\) , CD גובה המשולש.
\(S_{ACB}=\large\frac{AB\cdot CD}{2}=\large\frac{7\cdot 4}{2}\)
דרך ב
חישוב השטחים של משולשים ACD ו- CBD.
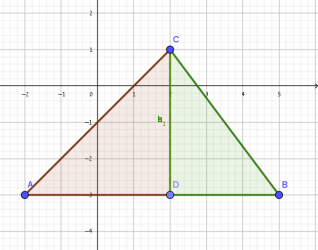
דרך ג
חישוב שטח המלבן EFBA והפחתת שטחי המשולשים ECA ו- CFB.
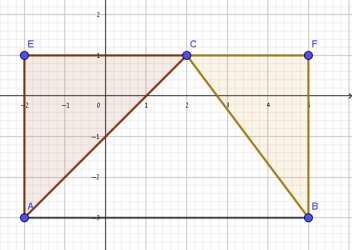
דרך ד
מציאת שיעורי נקודה H – נקודת החיתוך של ישר CB עם ציר ה- x .
מציאת השטחים של המשולשים CGH, AIG, HJB ושטח המלבן GHJI.
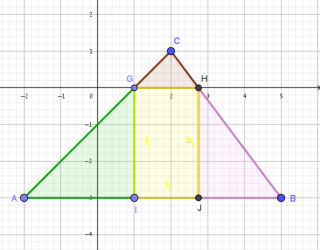
סעיפים ב' ו-ג'
כל הנקודות על הישרים \(y=1\space\space,\space\space y=-7\) (חוץ מנקודה C)