קטעים שווים במלבן - למורה
משימה
ABCD הוא מלבן.
\(E\) ו-\(F\) הן נקודות על ישר \(BC\) כך ש: \(AE=DF\).
- סרטטו סרטוט בהתאם לנתונים, התייחסו לאפשרויות שונות למיקום של נקודות \(E\) ו- \(F\).
- מצאו קטעים שווים בכל אחד מהסרטוטים שהצגתם, נמקו תשובתכם בדרכים שונות.
- מצאו כמה מרובעים אפשר למצוא בכל אחד מהסרטוטים שהצגתם.
מדרגה 1
- היעזרו ביישומון המצורף.
מדרגה 2
- לפניכם סרטוט אחד אפשרי. סרטטו עוד סרטוטים אפשריים:

- ניתן לרשום שמות מצולעים/קטעים בשדות המתאימים בתחתית היישומון (במקום "Empty").
- בחירה ב"צבע" תצבע את שטח המצולע.
- בחירה ב"שטח" תציג את שטח המצולע ובחירה ב"גודל" תציג את אורך הקטע.
- ניתן לגרור את הקודקודים A, B, E ולשנות את הצלעות.
- ניתן לבחור ב"מצב נוסף" ולהציג סרטוט אפשרי נוסף.
הנחיות למורה
כיתה מומלצת
- כיתה ט', שליש שני.
סוג המשימה
- תשובות מרובות.
- דרכים שונות.
הידע הדרוש
- תכונות מרובעים.
- ארבעת משפטי חפיפת משולשים.
מה נלמד
- העמקה וחידוד בנושא חפיפת משולשים.
- הבנה וחידוד בנושא מרובעים.
הדגשים ומטרות
- ניתוח נתונים, סרטוט והסקת מסקנות.
דירוג אתגר מתמטי
- הפנייה ליישומון.
- הצגת אחת מהאפשרויות לסרטוט מתאים לנתונים.
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות).
- דיון כיתתי על סעיפי א' וב' בו התלמידים יציגו את תשובותיהם וינמקו.
- על סעיף ג' ניתן לארגן תחרות קבוצתית. הקבוצה שתמצא הכי הרבה מרובעים תנצח.
הצעה לפתרון בהתאם לאחת מהאפשרויות:
א. סרטוט אפשרי:
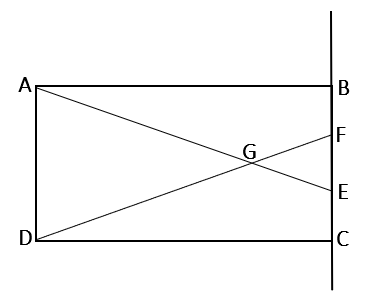
ב. קטעים שווים בסרטוט: \(AG=GD, GE=GF, BE=CF, BF=EC\)
דרכי פתרון אפשריות:
דרך אחת: להתחיל בחפיפת משולשים \(\triangle BAE\cong \triangle CDF\),
ומכאן להסיק לגבי שוויון קטעים וזוויות ולהסיק לגבי משולשים שווי שוקיים.
דרך אחרת: להוסיף לסרטוט את הקטעים \(AF\), ו- \(DE\).
טרפז \(AFED\) הוא טרפז שווה שוקיים ומכאן להסיק שוויון קטעים
ולהמשיך בחפיפת משולשים: \(\triangle AFG\cong \triangle DEG\).
ג. המרובעים בסרטוט הם:
\(AFED\) – טרפז שווה שוקיים,
\(CEAD, BFDA, DCFA, ABED\) – טרפזים ישרי זווית
\(ABCD\) – המלבן הנתון.


















