שטח והיקף של מעוין - למורה
משימה
- מה הוא שטחו של מעוין אשר היקפו 40 ס"מ? נמקו תשובתכם.
- האם קיים מעוין בעל היקף של 40 ס"מ ששטחו גדול משטח של כל מעוין אחר בעל היקף 40 ס"מ?
אם כן, מה שטחו? אם לא, הסבירו. - מבין כל המעוינים שהיקפם 40 ס"מ האם קיים מעוין בעל השטח הקטן ביותר? נמקו.
מדרגה 1 (לסעיפים א, ב, ג)
- היעזרו ביישומון המצורף.
מדרגה 2 (לסעיפים א, ב)
- האם קיים מעוין שהיקפו הוא 40 ס"מ, ושטחו שווה ל-80 סמ"ר? נמקו את תשובתכם.
- האם קיים מעוין שהיקפו הוא 40 ס"מ, ושטחו שווה ל-150 סמ"ר? נמקו את תשובתכם.
- גרירת קודקודי המעוין, A, C, D, משנה את המעוין או מזיזה אותו.
- בחלק התחתון של היישומון, ניתן לראות כיצד שינוי זווית D משפיע על שטח המעוין.
משימה נוספת – למצטיינים
- מבין כל המעוינים שהיקפם 4a ס"מ מצאו את שטח המעוין בעל השטח הגדול ביותר?
בטאו את התשובה בעזרת a. נמקו את תשובתכם. - מבין כל המעוינים שהיקפם 4a ס"מ האם קיים מעוין בעל השטח הקטן ביותר? נמקו.
מדרגה
- היעזרו ביישומון המצורף.
- לשינוי היקף המעוין היעזרו בסרגל הגרירה "אורך הצלע".
- גרירת קודקודי המעוין, A, C, D, משנה את המעוין או מזיזה אותו.
- בחלק התחתון של היישומון, ניתן לראות כיצד שינוי זווית D משפיע על שטח המעוין.
הנחיות למורה
כיתה מומלצת
- כיתה ט', שליש שני.
סוג המשימה
- משימת חקר.
- מדוגמאות להכללה.
- משימה בעלת תשובות רבות בתחום מסוים.
- קישור בין תחום שונים: גאומטריה ואלגברה.
הידע הדרוש
- תכונות של מעוין.
- תכונות של משולש ישר זווית.
- בניית ביטוי אלגברי.
מה נלמד
- הבנה כי קיימים מעוינים רבים בעלי אותו היקף.
- הבנה כי מעוינים שהיקפם שווה, שטחם לא בהכרח שווה.
- גילוי שבין כל המעוינים בעלי היקף שווה, ריבוע הוא בעל השטח הגדול ביותר.
- גילוי שבין כל המעוינים בעלי היקף שווה, לא קיים מעוין בעל שטח הקטן ביותר.
הדגשים ומטרות
- התמודדות עם משימת חקר, כלומר יש אין סוף מעוינים בעלי היקף נתון, אבל שטחם שונה.
דירוג אתגר מתמטי
- המשימה מדורגת ומובילה מדוגמאות להכללה בעזרת ביטוי אלגברי.
- הפנייה לשימוש ביישומון.
- הפנייה למתן דוגמאות.
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות). המורה יכול לנתב את התלמידים לשימוש במדרגות, או לאפשר לתלמידים להיעזר במדרגות בהתאם לרצונם.
- דיונים כיתתיים: התלמידים יציגו את הפתרונות השונים ויסיקו מסקנות בהתאם לסעיפים השונים של המשימה.
הצעות לפתרונות:
סעיף א
\(ר"מס\space0\lt S\le ר"מס\space100\)
שטח מעוין שהיקפו 40 ס"מ יכול להיות כל מספר בין 0 סמ"ר ל- 100 סמ"ר כולל 100 סמ"ר.
הסברים והדגשים
- יתכן ומעוינים בעלי היקפים שווים הם בעלי גבהים שונים, ואז שטחם שונה.
- הסבר אחר: בכל אחד מהמעוינים שהיקפם שווה יתכן והזווית בין שתי צלעות סמוכות שונה ואז שטחם שונה.
ניתן להסביר בעזרת דוגמאות מספריות.
ניתן להסביר בעזרת סרטוטים מתאימים.
ניתן להמחיש בעזרת כלים טכנולוגיים (קיים יישומון), או בעזרת סרגלים, עפרונות, קיסמים וכו'.
לדוגמא: שני מעוינים בעלי היקף שווה ושטח שונה.
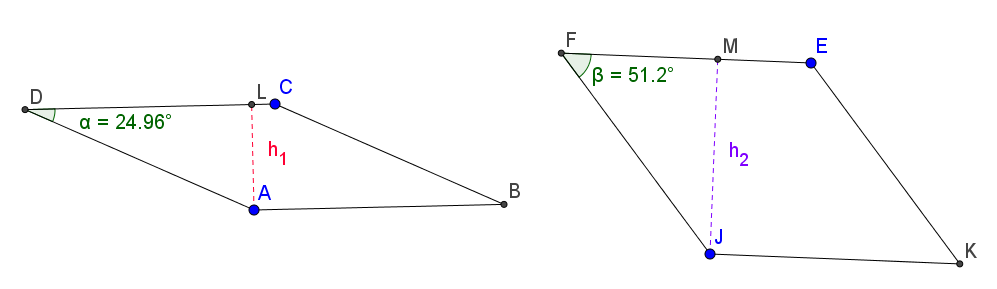
הסבר לסעיפים א' וב'
גובה מעוין שהיקפו 40 ס"מ לא יכול להיות גדול מ- 10 ס"מ (היתר במשולש ישר זווית הוא הצלע הגדולה ביותר במשולש – ראו לדוגמא במשולשים ADL ו- JFM).
ולכן השטח הגדול ביותר של מעוין שהיקפו 40 ס"מ הוא 100 סמ"ר – גובה המעוין מתלכד עם צלעו ומתקבל ריבוע.
הסבר נוסף בעזרת השוואת שטחים
ראו סרטוט למטה:

DIEJ הוא מעוין. המלבן OIET שטחו שווה לשטח המעוין (\(\triangle OID \cong \triangle TEJ\) ולכן הם שווי שטח).
הריבוע MIEN בנוי על צלע המעוין לכן היקפו שווה להיקף המעוין, אך שטחו גדול משטח המלבן ולכן גדול משטח המעוין.
כלומר הריבוע הוא בעל השטח הגדול ביותר מבין כל המעוינים בעלי היקף קבוע.
סעיפים ב' וג' ותשובות למשימה למצטיינים
- מבין כל המעוינים שהיקפם 4a ס"מ המעוין בעל שטח הגדול הוא ריבוע ושטחו \(a^2\) סמ"ר.
- לא קיים מעוין בעל השטח הקטן ביותר, כיוון שניתן להקטין את גובה המעוין עוד ועוד, כך ששטח המעוין יקטן עוד ועוד (קשור להקטנת הזווית בין שתי הצלעות הסמוכות של המעוין)


















