אלכסונים במרובע - למורה
משימה
בפעילות זו תחקרו ארבע קבוצות של מרובעים:
- מרובעים שאלכסוניהם שווים באורכם ומאונכים זה לזה.
- מרובעים שאלכסוניהם שווים באורכם אך לא מאונכים זה לזה.
- מרובעים שאלכסוניהם מאונכים זה לזה אך שונים באורכם.
- מרובעים שאלכסוניהם שונים באורכם וגם לא מאונכים זה לזה.
שאלה 1
- נתונים שני קטעים שווים באורכם.
נתון שאורך כל קטע הוא 5 ס"מ.
I. אם נניח את הקטעים האלה כך שיהיו מאונכים זה לזה, וניצור מרובע שהקטעים האלה הם אלכסוניו – אילו מרובעים נוכל לקבל?
II. האם יש תכונה שהיא משותפת לכל המרובעים שיכולים להתקבל?
אם כן – תארו אותה.
III. האם תשובותיכם לסעיפים הקודמים נכונות גם למקרה שאורך הקטעים
שונה מ-5 ס"מ? אם לא – מה משתנה בתשובותיכם? - נתונים שני קטעים שווים באורכם.
נתון שאורך כל קטע הוא 5 ס"מ.
I. אם נניח את הקטעים האלה כך שלא יהיו מאונכים זה לזה, וניצור מרובע
שהקטעים האלה הם אלכסוניו – אילו מרובעים נוכל לקבל?
II. האם יש תכונה שהיא משותפת לכל המרובעים שיכולים להתקבל?
אם כן – תארו אותה.
III. האם תשובותיכם לסעיפים הקודמים נכונות גם למקרה שאורך הקטעים
שונה מ-5 ס"מ? אם לא – מה משתנה בתשובותיכם?
שאלה 2
- נתונים שני קטעים שונים באורכם.
נתון שאורכי הקטעים הם 5 ס"מ ו-7 ס"מ.
I. אם נניח את הקטעים האלה כך שיהיו מאונכים זה לזה, וניצור מרובע
שהקטעים האלה הם אלכסוניו – אילו מרובעים נוכל לקבל?
II. האם יש תכונה שהיא משותפת לכל המרובעים שיכולים להתקבל?
אם כן – תארו אותה.
III. האם תשובותיכם לסעיפים הקודמים נכונות גם למקרה שאורכי הקטעים
שונים מ-5 ס"מ ו-7 ס"מ? אם לא – מה משתנה בתשובותיכם? - נתונים שני קטעים שונים באורכם.
נתון שאורכי הקטעים הם 5 ס"מ ו-7 ס"מ.
I. אם נניח את הקטעים האלה כך שלא יהיו מאונכים זה לזה, וניצור מרובע
הקטעים האלה הם אלכסוניו – אילו מרובעים נוכל לקבל?
II. האם יש תכונה שהיא משותפת לכל המרובעים שיכולים להתקבל?
אם כן – תארו אותה.
III. האם תשובותיכם לסעיפים הקודמים נכונות גם למקרה שאורכי הקטעים
שונים מ-5 ס"מ ו-7 ס"מ? אם לא – מה משתנה בתשובותיכם?
מדרגות לשאלות 1, 2
- תוכלו לבנות מרובעים שונים בעזרת: קשי שתיה/עטים/עפרונות…
או בעזרת היישומון או בעזרת כלים טכנולוגיים אחרים.
(ניתן ללחוץ על התמונות הבאות ולהגדילן)
- שימו לב שניתן לשנות את נקודת החיתוך בין האלכסונים.
- מה ניתן לדעת על מרובע שאלכסוניו מאונכים?
- ניתן להיעזר בנתונים מספריים לגבי אורכי האלכסונים בכל סעיף.
- לפי הצורך ניתן להיעזר במשפט פיתגורס.
- היעזרו ביישומון למדידות קטעים ושטחים.
יישומון לשאלה 1א – שווים ומאונכים
- ניתן לשנות את המרובע על ידי גרירת הנקודות \(A\), \(B\), \(E\).
- למדידת קטעים הקלידו בתיבות המתאימות (בחלון התחתון) את שמות נקודות הקצה של הקטע (באותיות גדולות), הקישו \(Enter\) ואחר כך הקישו על הכפתור "גודל".
יישומון לשאלה 1ב – שווים ואינם מאונכים
- ניתן לשנות את המרובע על ידי גרירת הנקודות \(A\), \(B\), \(E\).
- גרירת הסימון "סיבוב", משנה את המרובע ומשפיעה על שינוי הערכים הנמדדים (זוויות, אורכי קטעים וכו').
- למדידת קטעים הקלידו בתיבות המתאימות (בחלון התחתון) את שמות נקודות הקצה של הקטע (באותיות גדולות), הקישו \(Enter\) ואחר כך הקישו על הכפתור "גודל".
יישומון לשאלה 2א – אינם שווים אבל מאונכים
- ניתן לשנות את המרובע על ידי גרירת הנקודות \(A\), \(B\), \(E\).
- למדידת קטעים הקלידו בתיבות המתאימות (בחלון התחתון) את שמות נקודות הקצה של הקטע (באותיות גדולות), הקישו \(Enter\) ואחר כך הקישו על הכפתור "גודל".
יישומון לשאלה 2ב – אינם שווים ואינם מאונכים
- ניתן לשנות את המרובע על ידי גרירת הנקודות \(A\), \(B\), \(E\).
- גרירת הסימון "סיבוב", משנה את המרובע ומשפיעה על שינוי הערכים הנמדדים (זוויות, אורכי קטעים וכו').
- למדידת קטעים הקלידו בתיבות המתאימות (בחלון התחתון) את שמות נקודות הקצה של הקטע (באותיות גדולות), הקישו \(Enter\) ואחר כך הקישו על הכפתור "גודל".
הנחיות למורה
כיתה מומלצת
- כיתה ט', שליש שני.
סוג המשימה
- ריבוי תשובות.
- משימת חקר.
- גילוי והסקת מסקנות מתוך התשובות המתקבלות.
הידע הדרוש
- סוגים שונים של מרובעים ותכונותיהם.
- שטחים של משולשים ומרובעים.
מה נלמד
- חידוד והעמקה בתכונות של מרובעים, בדגש על הקשרים בין מאפיינים של אלכסונים לסוגי מרובעים.
- חידוד והעמקה של הקשר בין אלכסונים של מרובע המאונכים זה לזה לבין שטח המרובע.
הדגשים ומטרות
- תנאים מספיקים ליצירת מרובעים שונים בהקשר לאלכסונים.
- אלכסונים שווים אינה תכונה מספקת למלבן/ טרפז שווה שוקיים, גם במרובע כלשהו יכולים להיות אלכסונים שווים.
- במרובע כלשהו אלכסונים יכולים להיות מאונכים זה לזה.
- כל מרובע שאלכסוניו מאונכים זה לזה ניתן למצוא את שטחו על ידי מחצית מכפלת אלכסוניו. לכן כל המרובעים בעלי אותם אלכסונים ושאלכסוניהם מאונכים הם בעלי אותו שטח.
דירוג אתגר מתמטי
- הפנייה לשימוש באמצעי המחשה או עזרים טכנולוגיים.
- תזכורת לגבי הקשר בין שטח מרובע לאלכסוניו, כאשר האלכסונים מאונכים זה לזה.
- תזכורת לגבי שימוש במשפט פיתגורס.
מערך דידקטי מומלץ
- פתיחת השיעור: הצגת המשימה והנדרש בה.
- עבודה עצמית של התלמידים (ביחידים, בזוגות או בקבוצות). המורה יכול לנתב את התלמידים לשימוש במדרגות, או לאפשר לתלמידים להיעזר במדרגות בהתאם לרצונם.
- דיונים כיתתיים: התלמידים יציגו את הפתרונות השונים ויסיקו מסקנות בהתאם לסעיפים השונים של המשימה.
הצעות לפתרונות:
שאלה 1
שאלה 1 סעיף א/I
ניתן לקבל את המרובעים הבאים:
- ריבוע – אם בנוסף האלכסונים חוצים זה את זה.
- דלתונים – אם בנוסף רק אלכסון אחד חוצה את האלכסון השני.
- טרפזים שווי שוקיים – אם בנוסף האלכסונים מחלקים זה את זה כך שקטעי האלכסונים הקרובים לאותו בסיס שווים (או שהאלכסונים מחלקים זה את זה ביחס שווה).
- מרובעים כלשהם – אם לא מתקיימים תנאים נוספים.
שאלה 1 סעיף א/II
תכונות משותפות לכל המרובעים המתקבלים בסעיף א/I.
- כל המרובעים שווי שטח.
- סכום ריבועי זוג צלעות נגדיות אחד שווה לסכום ריבועי זוג צלעות נגדיות שני (ראו פתרון שאלה 2, סעיף א/II).
שאלה 1 סעיף א/III
התשובות לסעיפים הקודמים לא משתנות.
שאלה 1 סעיף ב/I
ניתן לקבל את המרובעים הבאים:
- מלבנים – אם בנוסף האלכסונים חוצים זה את זה.
- טרפזים שווי שוקיים – אם בנוסף האלכסונים מחלקים זה את זה כך שקטעי האלכסונים הקרובים לאותו בסיס שווים (או שהאלכסונים מחלקים זה את זה ביחס שווה).
- מרובעים כלשהם – אם לא מתקיימים תנאים נוספים.
שאלה 1 סעיף ב/II
אין תכונה משותפת לכל המרובעים שמתקבלים בסעיף ב/I.
שאלה 1 סעיף ב/III
התשובות לסעיפים הקודמים לא משתנות.
שאלה 2
שאלה 2 סעיף א/I
ניתן לקבל את המרובעים הבאים:
- מעוין – אם בנוסף האלכסונים חוצים זה את זה.
- דלתונים – אם בנוסף אלכסון אחד חוצה את האלכסון השני.
- טרפזים כלשהם – אם בנוסף האלכסונים מחלקים זה את זה ביחס שווה.
מרובעים כלשהם – אם לא מתקיימים תנאים נוספים.
שאלה 2 סעיף א/II
תכונות משותפות לכל המרובעים המתקבלים בסעיף ג:
- כל המרובעים שווי שטח.
- סכום ריבועי זוג צלעות נגדיות אחד שווה לסכום ריבועי זוג צלעות נגדיות שני.
\(AC^2+DB^2=BC^2+AD^2=CE^2+AE^2+EB^2+ED^2\)
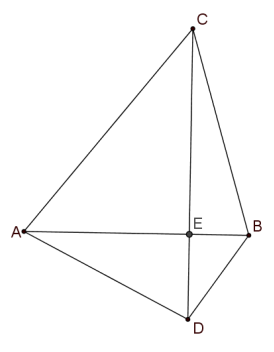
שאלה 2 סעיף א/III
התשובות לסעיפים הקודמים לא משתנות.
שאלה 2 סעיף ב/I
ניתן לקבל את המרובעים הבאים:
- מקביליות – אם בנוסף האלכסונים גם חוצים זה את זה.
- טרפזים כלשהם – אם בנוסף האלכסונים מחלקים זה את זה ביחס שווה.
- מרובעים כלשהם – אם לא מתקיימים תנאים נוספים.
שאלה 2 סעיף ב/II
אין תכונה משותפת לכל המרובעים שמתקבלים בסעיף ב/I.
שאלה 2 סעיף ב/III
התשובות לסעיפים הקודמים לא משתנות.
סיכום הפתרונות
| מספר שאלה | תכונות המרובעים | סעיף \(I\) סוגי מרובעים |
|---|---|---|
| שאלה 1 סעיף א | אלכסונים שווים ומאונכים | \(\small\circ\) ריבוע \(\small\circ\) דלתון \(\small\circ\) טרפז שווה שוקיים \(\small\circ\) מרובע כלשהו |
| שאלה 1 סעיף ב | אלכסונים שווים ואינם מאונכים | \(\small\circ\) מלבן \(\small\circ\) טרפז שווה שוקיים \(\small\circ\) מרובע כלשהו |
| שאלה 2 סעיף א | אלכסונים שונים באורכם ומאונכים | \(\small\circ\) מעוין \(\small\circ\) טרפז \(\small\circ\) דלתון \(\small\circ\) מרובע כלשהו |
| שאלה 2 סעיף ב | אלכסונים שונים באורכם ואינם מאונכים | \(\small\circ\) מקבילית \(\small\circ\) טרפז \(\small\circ\) מרובע כלשהו |





















